Jonathan Borwein, CARMA, University of Newcastle, Australia

Long before current graphic, visualisation and geometric tools were available, John E. Littlewood (1885-1977) wrote in his delightful A mathematician's miscellany (Methuen 1953):

"A heavy warning used to be given [by lecturers] that pictures are not rigorous; this has never had its bluff called and has permanently frightened its victims into playing for safety. Some pictures, of course, are not rigorous, but I should say most are (and I use them whenever possible myself)."

Over the past five to ten years, the role of visual computing in my own research has expanded dramatically. In part this was made possible by the increasing speed and storage capabilities - and the growing ease of programming - of modern multi-core computing environments. But, at least as much, it has been driven by my group's paying more active attention to the possibilities for graphing, animating or simulating most mathematical research activities. Part I. I shall first discuss briefly what is meant both by visual theorems and by experimental computation. I will then turn to dynamic geometry (iterative reflection methods) and matrix completion problems. Part II. I end with a description of recent work from my group in probability (behaviour of short random walks) and transcendental number theory (normality of real numbers).

Patrick Fowler, Department of Chemistry, University of Sheffield

Some graph-theory based models of currents induced in molecules by a magnetic field (ring currents) or potential difference (ballistic conduction) will be described, with case histories showing the interplay between chemical ideas, mathematical experimentation and computer search. This talk is based on joint work with Wendy Myrvold, Barry Pickup, Irene Sciriha.

Branden Fitelson, Philosophy, Northeastern University

I will do two things in this talk: (1) present an axiomatic generalization of Gibbard's (logical) triviality result for indicative conditionals, and (2) present an algebraic strengthening of Lewis's (probabilistic) triviality result for indicative conditionals. Both results start from a very weak background theory (either logical or probabilistic) of the indicative conditional, and (relative to these weak backgrounds) both results will rely only on the so-called Import-Export Law. So, these results can be viewed as (general, and strong) "odd consequences" of Import-Export. As I will explain in the talk, the use of automated theorem provers, model finders, and decision procedures was essential to the discovery and verification of all of these new results.

Austin Roche, Maplesoft, Waterloo

Lila Kari , Department of Computer Science, University of Waterloo

Approaches to understanding and utilizing the mathematical properties of bioinformation take many forms, from using DNA to build lattices and polyhedra, to studies of algorithmic DNA self- assembly, and harnessing DNA strand displacement for biocomputations. This talk presents a view of the structural properties of DNA sequences from yet another angle, by proposing the use of Chaos Game Representation (CGR) of DNA sequences to measure and visualize their interrelationships. The method we propose computes an “information distance” for each pair of Chaos Game Representations of DNA sequences, and then uses multidimensional scaling to visualize the resulting interrelationships in a three-dimensional space. The result of applying it to a collection of DNA sequences is an easily interpretable 3D Molecular Distance Map wherein sequences are represented by points in a common Euclidean space, and the spatial distance between any two points reflects the differences in their subsequence composition. This general-purpose method does not require DNA sequence alignment and can thus be used to compare similar or vastly different DNA sequences, genomic or computer-generated, of the same or different lengths. Our most recent results indicate that while mitochondrial DNA signatures can reliably be used for species classification, conventional CGR signatures of nuclear genomic sequences do not always succeed to separate them by their organism of origin, especially for closely related species. To address this problem, we propose the general concept of additive DNA signature of a set of DNA sequences, which combines information from all the sequences in the set to produce its signature, and show that it successfully overcomes the limitations of conventional genomic signatures.

Yuri V. Matiyasevich, St. Petersburg Department of the Steklov Institute for Mathematics

In 2011, the speaker began to work with finite Dirichlet series of length N vanishing at N −1 initial non-trivial zeroes of Riemann’s zeta function. Intensive multiprecision calculations revealed several interesting phenomena. First, such series approximate with great accuracy the values of the product (1 − 2 · 2^(-s)) zeta(s) ζ(s) for a large range of s lying inside the critical strip and to the left of it (even better approximations can be obtained by dealing with ratios of certain finite Dirichlet series). In particular the series vanish also very close to many other non-trivial zeroes of the zeta function (initial non-trivial zeroes “know about” subsequent non-trivial zeroes). Second, the coefficients of such series encode prime numbers in several ways. So far no theoretical explanation has been given for the observed phenomena. The ongoing research can be followed at http://logic.pdmi.ras.ru/~yumat/personaljournal/finitedirichlet

David Linder, Maplesoft, Waterloo

The Maple computer algebra system has a programmatically accessible database of interrelated special function identities and conversion rules. This can be used for simplification and reformulation of expressions. While Maple's `simplify` command makes some use of this knowledge this facility is not exhaustive. Identities hitherto unknown to the system may be programmatically generated, as illustrated by example. The question of how to augment the database, in part by programmatic search and computation, is discussed.

Ernest Davis, Department of Computer Science, New York University

In mathematics, large parts of the project initiated by Whitehead and Russell have been accomplished. Using theorem-verification technology, online libraries of mathematical proofs have been assembled which go all the way from foundational axioms to very deep theorems. Suppose that you want to do the same thing for physics; and suppose that you want the foundational point to be, not the fundamental laws of physics as we have determined them, but the experiments and observations from which the laws are derived. What would such a derivation look like? I will discuss some aspects of how such a project could reasonably be formulated, and what would be involved in it.

Ann Johnson , Department of Science & Technology Studies, Cornell University

The ability to make reliable predictions based on robust and replicable methods is possibly the most distinctive and important advantage claimed about scientific knowledge versus other types of knowledge. Because of the common use of computers and computational tools prediction in science and engineering is playing a much more important and ever-present role in 21st century knowledge production. Computers and simulation methods play prominent roles in a wide range of present-day scientific and engineering research. Without doubt, the computer, computational science, and scientific and engineering research have all mutually shaped one another—what is computationally possible informs the questions scientists and engineers ask and the questions scientists and engineers ask, in part, shape the development of new hardware and software. These mutual influences have been frequently examined, largely through the origins of scientific computing and the application of computers to a series of scientific disciplines and problems in the 1940s and 50s. However, I want to focus on a even more recent development. Namely, to argue that the wide and relatively cheap availability of computing power, particularly through mature networked desktop computing or the so-called “PC (personal computer) Revolution,” has triggered—but, to be clear, not made inevitable—a reorientation in the practices of scientists and engineers. My thesis is that substantial changes have occurred in research practices and culture over the past decades and that these developments have been made possible by everyday accessibility to simulation methods by a wide variety of technical actors. Furthermore, these changes help to generate a highly exploratory mode of research, which, in turn, amplifies the character and role of prediction in science. Such exploratory and iterative strategies introduce a design mode of knowledge production, where science becomes more engineering-like by focusing on 1) making things virtually and 2) testing their performance in computer simulations, and refining design. This is true of obvious engineering designs like planes, but also of molecules, economies, and seemingly autonomous traffic patterns. This new orientation towards design and prediction challenges some of the basic tenets of the philosophy of science, in which scientific theories and models are predominantly seen as explanatory rather than predictive. This talk will use examples from computational fluid dynamics, computational chemistry, and population biology to show what the new computational culture of prediction looks like and what it may mean.

Jim Brown, Department of Philosophy, University of Toronto

Philosophers of mathematics and working mathematicians distinguish pure and applied mathematics differently. Both distinctions are legitimate and useful in their ways. The mathematicians’ distinction has interesting similarities to ethics, which will be explored. This in turn leads to some interesting consequences, especially when it comes to how mathematical claims are justified: proofs, experimental computations, thought experiments, and so on.

Neil J. A. Sloane, OEIS Foundation, and Department of Mathematics, Rutgers University

The On-Line Encyclopedia of Integer Sequences is 52 years old, contains 270,000 sequences, and has been cited by 4700 artcles, many saying "this discovery was made with the help of the OEIS". I will give example of such discoveries, as well as recent sequences that are begging to be analyzed and are guaranteed to cause loss of sleep. There will be music and a movie.

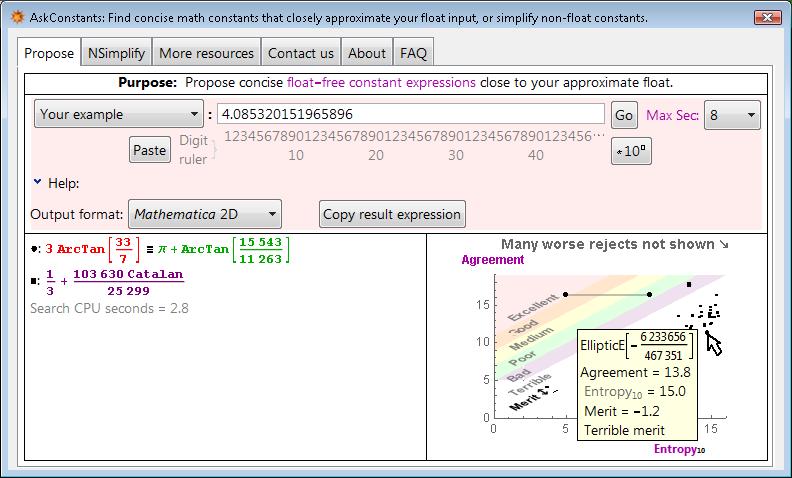
David Stoutemyer, Department of Information and Computer Science, University of Hawaii

David H. Bailey , Lawrence Berkeley National Lab and University of California, Davis

In two earlier studies of lattice sums arising from the Poisson equation of mathematical physics, we established that the lattice sum phi_2(x,y) = 1/pi*log A, where A is an algebraic number. We were also able to compute the explicit minimal polynomials associated with A for a few specific rational arguments x and y. Based on these results, Jason Kimberley conjectured a number-theoretic formula for the degree of A in the case x = y = 1/s for some integer s. These earlier studies were hampered by the enormous cost and complexity of the requisite computations. In this study, we address the Poisson polynomial problem with significantly more capable computational tools: (a) a new thread-safe arbitrary precision package; (b) a new three-level multipair PSLQ integer relation scheme; and (c) a parallel implementation on a 16-core system. As a result of this improved capability, we have confirmed that Kimberley's formula holds for all integers s up to 50 (except for s = 41, 43, 47, 49, which are still too costly to test). As far as we are aware, these computations, which employed up to 51,000-digit precision, producing polynomials with degrees up to 324 and integer coefficients up to 10^145, constitute the largest successful integer relation computations performed to date. The resulting polynomials have some interesting features, such as the fact that when s is even, the polynomial is palindromic (i.e., coefficient a_k = a_{d-k}), where d is the degree). Further, by examination of these polynomials, we have found connections to a sequence of polynomials defined in a 2010 paper by Savin and Quarfoot.

Thirty Minute Talks (Alphabetical by Last Name)

Tanbir Ahmed, LaCIM, UQAM,

Ramsey Theory has been a hard but exciting area in mathematics for decades.Theoretical results in this broad area draw significant attention due to the inherently difficult nature of the problems. For the same reason, discovering Ramsey-type extremal combinatorial objects, such as graphs and numbers, continues to challenge computer scientists and mathematicians. Recently, computer experiments and explorations have not only allowed us to discover patterns and properties with further insight into those extremal problems, but also have helped us to re-kindle the excitement, particularly among young mathematicians and computer scientists. In this talk, I present some results in Ramsey theory on the Integers and Zero-sum Ramsey theory obtained through mathematical experimentations.

Max A. Alekseyev, Department of Mathematics, George Washington University

We present computational methods for solving Diophantine equations of two forms:

A*P^m + B*Q^n +C*R^k = 0 and A*m^2 + B*m + C = D*Q^n,

where $A,B,C,D,P,Q,R$ are given integers, $P,Q,R>0$, and $m,n,k$ are unknowns. The methods are based on modular arithmetics and aimed at bounding values of the variables, which further enables solving the equations by exhaustive search. We illustrate the methods workflow with some Diophantine equations like 4 + 3^n - 7^k = 0 and 2*m^2 + 1 = 3^n and show how one can compute all their solutions.

Bert Baumgaertner, Department of Philosophy, University of Idaho

The Voter Model and variations of it are used to study the mathematical principles of opinion dynamics. Common aims in this area include the calculation of the probability of reaching consensus, time to consensus, distribution of cluster sizes, etc. We introduce a stochastic spatial agent-based model of opinion dynamics that includes a spectrum of opinion strengths and various possible rules for how the opinion type and strength of one individual affect the influence that individual has on others. Through simulations of the model, we find that even a small amount of amplification of opinion strength through interaction with like-minded neighbors can tip the scales in favor of polarization and dead- lock. Moreover, the spatial patterns that emerge and their dynamics resemble surface tension and motion by mean curvature. While these are also observed in the Threshold Voter Model, their emergence is the result of a very different mechanism. Finally, we compare the time dynamics of our spatial model with an ODE version.

Murray Bremner , Mathematics & Statistics, University of Saskatchewan

The starting point was to determine the number of inequivalent placements of operation symbols in a monomial of degree n generated by completely symmetric binary and ternary operations [-,-] and (-,-,-). Another way to visualize this is to consider directed rooted non-planar trees in which every internal node has in-degree 2 or 3: the leaves represent the arguments and the internal nodes represent the operations. Maple calculations produced this initial sequence:

1, 1, 2, 4, 9, 23, 58, 156, 426, 1194, 3393, 9802, ...,

which was not in the OEIS (it is now A268172). The next step was to determine the number of inequivalent multilinear mononomials of degree n: this is the sum, over all placements of operation symbols, of n! divided by the order of the group of symmetries of the placement. Further Maple calculations produced this initial sequence: 1, 1, 4, 25, 220, 2485, 34300, 559405, 10525900, 224449225, ..., which was not in the OEIS (it is now A268163). An internet search for the first few terms of this sequence revealed the remarkable fact that it also enumerates the number of Feynman diagrams involved with multi-gluon scattering in quantum chromodynamics. The underlying structure in both cases is the set of labeled binary-ternary directed rooted non-planar trees indexed by the number n of leaves. Further details on the connections with physics can be found in these surveys: B. Feng and M. Luo, An introduction to on-shell recursion relations, Review Article, Frontiers of Physics, October 2012, Volume 7, Issue 5, pp. 533-575. M. L. Mangano and S. J. Parke, Multi-parton amplitudes in gauge theories, Physics Reports, Volume 200, Issue 6, February 1991, pp. 301-367. In this talk I will show how these sequences were discovered, sketch the relation with nuclear physics, and describe an infinite family of other sequences which are also related to Feynman diagrams.

Curtis Bright, School of Computer Science, Waterloo University

In this talk, we present MathCheck2, a combination of a SAT solver and a computer algebra system (CAS) aimed at finitely verifying or counterexampling mathematical conjectures. Using MathCheck2 we generated Hadamard matrices all orders 4n with n < 35 and provided 160 matrices to the Magma Hadamard database that were not equivalent to any matrix previously in that database. Furthermore, we provide independent verification of the claim that Williamson matrices of order 35 do not exist, and demonstrate for the first time that 35 is the smallest number with this property. The crucial insight behind the MathCheck2 algorithm and tool is that a combination of an efficient search procedure (like those in SAT solvers) with a domain-specific knowledge base (à la CAS) can be a very effective way to verify, counterexample, and learn deeper properties of mathematical conjectures (especially in combinatorics) and the structures they refer to. MathCheck2 uses a divide-and-conquer approach to parallelize the search, and a CAS to prune away classes of structures that are guaranteed to not satisfy the conjecture-under-verification C. The SAT solver is used to verify whether any of the remaining structures satisfy C, and in addition learn UNSAT cores in a conflict-driven clause-learning style feedback loop to further prune away non-satisfying structures. (This is joint work by Curtis Bright, Vijay Ganesh, Albert Heinle, Ilias Kotsireas, Saeed Nejati, and Krzysztof Czarnecki)

Marc Chamberland, Grinnell College

Experimental Mathematics is the utilization of advanced computing technology in mathematical research for discovering new patterns and relationships, testing and falsifying conjectures, replacing lengthy hand derivations with the computer, and suggesting approaches for a formal proof. With support from the NSF, a course in Experimental Mathematics was developed and taught. The course is integrative (covers many different mathematical areas such as calculus, linear algebra, differential equations, combinatorics, analysis, etc.) and incorporates an REU-like research experience. This talk will present the guiding principles, structure and some detail of the course.

Shaoshi Chen , Key Laboratory of Mathematics Mechanization, Chinese Academy of Sciences

In 1992, Wilf and Zeilberger conjectured that a hypergeometric term in several discrete and continuous variables is holonomic if and only if it is proper. Strictly speaking the conjecture does not hold, but it is true when reformulated properly: Payne proved a piecewise interpretation in 1997, and independently, Abramov and Petkovsek in 2002 proved a conjugate interpretation. Both results address the pure discrete case of the conjecture. In this paper we extend their work to hypergeometric terms in several discrete and continuous variables and prove the conjugate interpretation of the Wilf-Zeilberger conjecture in this mixed setting. With the proof of this conjecture, one now could algorithmically detect the holonomicity of hypergeometric terms by checking properness with the algorithms in the work by Chen et al. This is important because it gives a simple test for the termination of Zeilberger's algorithm. This is joint work with Christoph Koutschan (Austrian Academy of Sciences).

Rob Corless, Department of Applied Mathematics, Western University

The BOunded HEight Matrix of Integers Eigenvalue project, or "Bohemian Eigenvalue Project" for short, has its original source in the work of Peter Borwein and Loki Jörgenson on visible structures in number theory (c 1995), which did computational work on roots of polynomials of bounded height (following work of Littlewood). Some time in the late 90's I realized that because their companion matrices also had bounded height entries, such problems were equivalent to a subset of the Bohemian eigenvalue problems. That they are a proper subset follows from the Mandelbrot matrices, which have elements {-1, 0} but whose characteristic polynomials have coefficients that grow doubly exponentially, in the monomial basis. There are a great many families of Bohemian eigenvalues to explore: companion matrices in other bases such as the Lagrange basis (my work here dates to 2004), general Bohemian dense matrices, circulant and Toeplitz matrices, complex symmetric matrices, and many more. The conference poster contains an image from this project. This talk presents some of our recent results. Joint work with Steven Thornton, Sonia Gupta, Jonny Brino-Tarasoff, and Venkat Balasubramanian

Karl Dilcher, Dalhousie University

We study analytic properties of the Witten zeta function ${\mathcal W}(r,s,t)$, which is also named after Mordell and Tornheim. In particular, we evaluate the function ${\mathcal W}(s,s,\tau s)$ ($\tau>0$) at $s=0$ and, as our main result, find the derivative of this function at $s=0$, which turns out to be surprisingly simple. These results were first conjectured using high-precision calculations based on an identity due to Crandall that involves a free parameter and provides an analytic continuation. This identity was also the main tool in the eventual proofs of our results. Finally, we derive special values of a permutation sum and study an alternating analogue of ${\mathcal W}(r,s,t)$. (Joint work with Jon Borwein).

Laureano Gonzalez-Vega , Departamento de Matematicas, Estadistica y Computacion, Universidad de Cantabria

Geometric entities such as the set of the real zeros of a bivariate equation f(x,y)=0 can be treated algorithmically in a very efficient way by using a mixture of symbolic and numerical techniques. This implies that it is possible to know exactly which is the topology (connected components and their relative position, connectedness, singularities, etc.) of such a curve if the defining equation f(x,y) is also known in an exact manner (whatever this means) even for high degrees. In this talk we would like to describe three different "experiments" that highlight how new visualization tools in Computational Mathematics mixing symbolic and numerical techniques allow to perform experiments conveying either to mathematical discoveries and/or to new computational techniques. The first experiment to consider is not successful yet: it deals with the first part of Hilbert's sixteenth problem asking for the relative positions of the closed ovals of a non-singular algebraic curve f(x,y)=0 (regarded in the real projective plane). The problem is solved for degrees less or equal to 7 and, despite several attempts by H. Hong and F. Santos for degree 8, experimentation here has not produced yet any insight. Second experiment was successful: for a long period, in Algebraic Geodesy, it was not known where Vermeille’s method failed when inverting the transformation from geodetic coordinates to Cartesian coordinates. In 2009 L. Gonzalez-Vega and I. Polo-Blanco were able to compute exactly the region where Vermeille’s method cannot be applied by analysing carefully the topology of the arrangement of several real algebraic curves defined implicitly (coming from the solution of a quantifier elimination problem according to the terminology in Real Algebraic Geometry). Finally, third experiment has a different nature. In Computer Aided Design, the computation of the medial axis (or skeleton) of a region in the plane whose boundary is the union of finitely many curves has a wide range of applications. If the curves defining the region to compute the medial axis are restricted to be segments or conic arcs then I. Adamou, M. Fioravanti and L. Gonzalez-Vega have been able to determine all the possible “topologies” for the curves appearing in the medial axis (information which is specially useful when computing it). Again, the key tool here was the computation of the topology of the bisector curves (which in general are not rational) appearing in the medial axis to be computed.

Wayne Grey, Department of Mathematics, Western University

My 2015 thesis solved nearly all cases of the inclusion problem for mixed Lebesgue norms in two variables, leaving only one specific case, with atomic measures and exponents in a particular order. Finding the best constant in this difficult case turns out to generalize the (NP-hard) optimizing version of the partition problem. A simple sufficient condition based on Minkowski's integral inequality is also necessary for nonatomic measures. Even for arbitrarily many variables, a combinatorial argument fully solves the problem with nonatomic measures by reducing it to two-variable subproblems. This talk focuses on the outstanding question of whether this Minkowski condition on two-variable subproblems is sufficient even with atomic measures. The analytic problem is translated into a combinatorial one, akin to bubble sort but more complicated, with a substitution move in addition to the adjacent swap. Computational experiments designed to find a counterexample eventually led me to conjecture that there isn't one, and gave insights which assist work by hand. Specifically, they showed that sometimes more exchanges are necessary than in bubble sort. The smallest such example has four variables and begins by swapping an initially in-order middle pair, which is swapped back later.

Kevin Hare, Department of Mathematics, University of Waterloo

We build upon previous work on the densities of uniform random walks in higher dimensions, exploring some properties of the even moments of these densities and extending a result about their evaluation modulo certain primes.

James Hughes, Department of Computer Science, Western University

The brain is an intrinsically nonlinear system, yet the dominant methods used to generate network models of functional connectivity from fMRI data use linear methods. Although these approaches have been used successfully, they are limited in that they can find only linear relations within a system we know to be nonlinear. This study employs a highly specialized genetic programming system which incorporates multiple enhancements to perform symbolic regression, a sophisticated and computationally rigorous type of regression analysis that searches for declarative mathematical expressions to describe relationships in observed data with any provided set of basis functions. Publicly available fMRI data from the Human Connectome Project were segmented into meaningful regions of interest and highly nonlinear mathematical expressions describing functional connectivity were generated. These nonlinear expressions exceed the explanatory power of traditional linear models and allow for more accurate investigation of the underlying physiological connectivities.

Sergey Khashin, Department of Mathematics, Ivanovo State University

The most powerful elementary probabilistic method for primality test is the Frobenius test. Frobenius pseudoprimes are the natural numbers for which this test fails. There are several slightly different definitions of Frobenius pseudoprimes (FPP), which are almost equivalent. We are using the following one. {\bf Definition} Frobenius pseudoprime (FPP) is a composite odd integer $n$ such that it is not a perfect square provided $ z^n \equiv \overline{z} \mod n$, where $z=1+\sqrt{c}$ and $c$ is the smallest odd prime number with the Jacobi symbol $J(c/n)=-1$. {\bf Theorem 1(multiple factors)}. Let $n=p^sq$ is FPP where $p$ is prime and $s>1$. Then ${z^p = \overline{z} \mod p^2}$. {\bf Experiment 1}. There are no exist such prime $p<2^{32}$. {\bf Theorem 2}. Let $n=pq$ be FPP where $J(c/p)=+1$. Then $z_1^q \equiv z_2$, $z_2^q \equiv z_1 \mod p$, where $z_{1,2} = 1 \pm d \mod p$ and $d^2 = c \mod p$. {\bf Experiment 2}. For each $c$ there exists a short list ($<20$) of such primes $p$. {\bf Experiment 3}. There exist no FPP less than $2^{60}$.

Craig Larson, Department of Mathematics and Applied Mathematics, Virginia Commonwealth UniversityDepartment

CONJECTURING is an open-source Sage program which can be used to make invariant-relation or property-relation conjectures for any mathematical object-type. The user must provide at least a few object examples, together with functions defining invariants and properties for that object-type. These invariants and properties will then appear in the conjectures. Here we demonstrate how the CONJECTURING program can be used to produce proof sketches in graph theory. In particular, we are interested in graphs where the independence number of the graph equals its residue. Residue is a very good lower bound for the independence number - and the question of characterizing the class of graphs where these invariants are equal has been of continuing interest. The CONJECTURING program can be used to generate both necessary and sufficient condition conjectures for graphs where the independence number equals its residue, and proof sketches of these conjectures can also be generated. We will discuss the program and give examples. This is joint work with Nico Van Cleemput (Ghent University).

Ao Li, Department of Applied Mathematics, Western University

In his 1991 paper "A Chaotic Search for i" [1], Gilbert Strang explores an analytical solution for the Newton iteration for f(x) = x^2+1 = 0 starting from real initial guesses, namely x_n = cot (2^n A_0). In this work we extend this to both Halley's method and the secant method, giving x_n = cot (3^n A_0) and x_n = cot A_n with A_n = A_{n-1} + A_{n-2} respectively. We describe several consequences (some of which illustrate some well-known features of iterative root-finding methods, and some of which illustrate novel facts) and speculate on just how far this can be taken.

[1] Strang G. The chaotic search for i. The College Mathematics Journal, 22(1):3-12, 1991.

Daniel Lichtblau, Wolfram Research

Recent work by Lemke Oliver and Soundararajan shows an unexpected asymmetry in distribution of last digits of consecutive primes. For example, in the first 10^8 pairs of consecutive primes, around 4.6 million end with {1,1} respectively, whereas more than 7.4 million end with {1,3}. It is not hard to show that his disparity is not explained by the fact that opportunities for the next prime come sooner for n+2 than for n+10. Which leaves open the question: what accounts for this sizable bias? In this talk I will give an explanation based on elementary theory and some amount of computation.

Scott Lindstrom, CARMA, University of Newcastle

We investigate some of the connections between continued fractions and continued logarithms. We study the binary continued logarithms as introduced by Bill Gosper and explore two generalizations of the continued logarithm to base b. We show convergence for them using equivalent forms of their corresponding continued fractions. Through numerical experimentation we discover that, for one such formulation, the exponent terms have finite arithmetic means for almost all real numbers. This set of means, which we call the logarithmic Khintchine numbers, has a pleasing relationship with the geometric means of the corresponding continued fraction terms. While the classical Khintchine's constant is believed not to be related to any naturally occurring number, we find surprisingly that the logarithmic Khintchine numbers are elementary. For another formulation of the generalization to base b, we obtain finite termination for rationals and discover a theoretical recursion for building the analogous distributions. This is a joint project with Jonathan Borwein, Neil Calkin, and Andrew Mattingly

Johannes Middeke, Research Institute for Symbolic Computation, Linz

In our recent project we have tackled the surprisingly frequent occurrence of common row factors in Bareiss' fraction-free algorithm for matrix LU decomposition. We used computer experiments to first confirm the existence of those factors and then to gain an idea about how they arise. We applied similar methods to the fraction-free QR decomposition. In this talk, we discuss our approach to incorporate experimental methods in finding rigorous proofs.

Rob Moir, Department of Applied Mathematics, Western University

Traditionally in philosophy of science, the process of discovery of theories or hypotheses in science has been regarded as being non-rational and therefore not accessible to philosophical scrutiny. For Reichenbach's famous epistemological distinction between the "context of discovery" (idea generation) and the "context of justification" (idea defense), it is the latter that is the focus of most philosophical scrutiny of science, and the former, in Reichenbach's view, only insofar as objective judgements of inductive evidential support can be made.[1] Indeed, Hempel (1985) stated that automatic genera- tion of interesting scientific hypotheses by computer is impossible.[2] With the advent of advanced computing machines and superior AI, this dogma is now coming into question.[3] Many philosophers of science now challenge this traditional view, and promote rational views of scientific discovery by emphasizing distinct structure to the discovery process, such as methodological patterns, analogical reasoning, mental modeling and reconstruction by explicit computation.[4] The approach I propose, which I believe is novel, could be construed as a mixture of the approaches just listed. I suggest that from a direct examination of historical evidence we can abstract a discovery pattern based on key aspects of the actual methods used, a pattern potentially limited by the range of evidence considered. I shall argue that the existence of this pattern shows not only that discovery processes can be rational but that they can even display an important algorithmic component. I will briefly review three examples of the discovery of important theories in physics (in optics, electromagetism and QED) and show how, subsequent to the identification of an appropriate problem space given empirical knowledge of the phenomenon, they all follow a pattern of recursive search through a problem space to solve a kind of inverse problem (combined with a refinement or variation of the characterization of the problem space).[5] These instances of success of a computational search method in several landmark discoveries in physics suggests that a deeper examination of the computational character of the discovery process in the history of science is needed.

[1] Glymour and Eberhardt, "Hans Reichenbach", The Stanford Encyclopedia of Philosophy, plato.stanford.edu/archives/fall2014/entries/reichenbach/.

[2] Hempel (1985) "Thoughts on the Limitations of Discovery by Computer".

[3] See, e.g., Schmidt and Lipson (2009) "Distilling Free-Form Natural Laws from Experimental Data", Science 324, 81, and Brunton, Proctor and Kutz (2015) "Discovering governing equations from data: Sparse identification of nonlinear dynamical systems", arXiv:1509.03580.

[4] Schickore, "Scientific Discovery", The Stanford Encyclopedia of Philosophy, plato.stanford.edu/archives/spr2014/entries/scientific-discovery/.

[5] There may be a case for modeling the examples in terms of the gradual formation and refinement of a (flexible) constraint satisfaction problem (CSP), followed by its solution, making a distinct connection to contemporary AI.

Mikhail Panine, Department of Applied Mathematics, University of Waterloo

The discipline of spectral geometry studies the relationship between the shape of a Riemannian manifold and the spectra of natural differential operators, mainly Laplacians, defined on it. Of particular interest in that field is whether one can uniquely reconstruct a manifold solely from knowledge of such spectra. This is commonly stated as “can one hear the shape of a drum?”, after Mark Kac's paper of the same title. Famously, the answer to this question is negative. Indeed, it has been shown that one can construct pairs of isospectral, yet non-isometric manifolds. However, it remains unknown how frequent such counterexamples are. It is expected that they are rare in some suitable sense. We explore this possibility by linearizing this otherwise highly nonlinear problem. This corresponds to asking a simpler question: can small changes of shape be uniquely reconstructed from the corresponding small changes in spectrum? We apply this strategy numerically to a particular class of planar domains and find local reconstruction to be possible if enough eigenvalues are considered. Moreover, we find evidence that pairs of isospectral non-isometric shapes are exceedingly rare.

Greg Reid, Department of Applied Mathematics, Western University

We consider classes of models specified by polynomial equations, or more generally polynomially nonlinear partial differential equations, with parametric coefficients. A basic task in computational discovery is to identify exceptional members of the class characterized by special properties, such as large solution spaces, symmetry groups or other properties. Symbolic algorithms such as Groebner Bases and their differential generalizations can some times be applied to such problems. These can be effective for systems with exact (e.g. rational) coefficients, but even then can be prohibitively expensive. They are unstable when applied to approximate systems. I will describe progress in the approximate case, in the new area of numerical algebraic geometry, together with fascinating recent progress in convex geometry, and semi-definite programming methods which extends such methods to the reals. This is joint work with Fei Wang, Henry Wolkowicz and Wenyuan Wu.

Gozde Sarikaya, Informatics Institute, Istanbul Technical University

Prime numbers are the main ingredient of the cryptosystems such as RSA, Elliptic Curve Cryptosystem etc. The critical aspect of RSA is the difficulty of factorization of large integers that have several hundred digits. It is not always easy to construct such large integers with large prime factors so that factoring is hard for these numbers. The first task is to determine the primality of an integer. One of the primality test algorithms that is being used in practice, Miller Rabin test, guarantee compositeness of most integers but it may fail to determine the compositeness of some. In this work, we test a conjecture by S. Ling et.al which adds a single condition to strong pseudoprime test to base 2. The test we conducted gives clues to pattern of strong pseudoprimes to base 2 and explains why the strong pseudo prime test base 2 with the additional condition catches all composite integers. We have been able to show that the test catches all composite integers to 10^20. In this work, we explain the algorithm in details and present our observation of the computational tests. The observation will show that why the conjectured primality test is actually a primality test. The conjectured primality test has running time of O(log^2 n) and it uses singular cubics.

Jeffrey Shallit, School of Computer Science, University of Waterloo

In this talk, I will show how to guess and prove theorems in combinatorics on words using the Walnut prover, written by Hamoon Mousavi. As an example, we recently proved the following result: the infinite word

r = 001001101101100100110110110010010011011001001001101100100100 ...

generated as the fixed point of the map a -> abcab, b -> cda, c -> cdacd, d -> abc, followed by the coding sending a, b -> 0 and c, d -> 1, is aperiodic and avoids the pattern x x x^R, where x^R denotes the reversal of x. This is the first nontrivial result on avoidance in words obtained through the use of a prover. This is joint work with Chen Fei Du, Hamoon Mousavi, Eric Rowland, and Luke Schaeffer.

Matthew Skerritt , University of Newcastle

Given a vector $(x_1,\dots, x_n)$ of real numbers, we say that an integer relation of that vector is a vector of integers $(a_1,\dots,a_n)$ with the property that $a_1 x_1 + \dots + a_n x_n = 0$. The PSLQ algorithm will compute (to within some precision) an integer relation for a given vector of floating point numbers. PSQL is also known to work in the case of finding gaussian integer relations for an input vector of complex numbers. We discuss recent endeavours to extend PSQL to find integer relations consisting of algebraic integers from some algebraic extension field (in either the real, or complex cases). Work to date has been entirely in quadratic extension fields. We will outline the algorithm, and discuss the required modifications for handling algebraic integers, problem that have arisen, and challenges to further work.

Pierluigi Vellucci, Dipartimento di Scienze di Base e Applicate per l'Ingegneria, Sapienza Universita di Roma

In this talk we describe a "mathematical experiment" that highlights some of the connections between nested square roots of 2 and the Gray code, a binary code employed in Informatics. The nested square roots considered here are obtained from the zeros of a particular class of orthogonal polynomials, which can be related to the Chebyshev polynomials. The expression of the zeros is

+-sqrt(2+-sqrt(2+-sqrt(+-2 ... sqrt(2))))

These polynomials are created by means of the iterative formula, L_n(x) = L^2_{n-1}(x)- 2, employed in Lucas-Lehmer primality test. The experiment is structured in the following steps: 1) we wonder what is the effect of + and - signs in the above expression, giving some preliminary considerations, conjectures and results; 2) we apply a "binary code" that associates bits 0 and 1 to + and - signs in the nested form above, and we numerically evaluate all the zeros of associated polynomial for n=2, n=3 (and so on); 3) an internet search on OEIS database for the first terms of this sequence reveals an ordering of nested square roots previously described, according to the Gray code; the decimal equivalent of Gray code for n on OEIS, is A003188; 4) we give the proof of the iterative formula.